Math Magic: Fun Tricks to Amaze and Educate Your Elementary Schooler!

Math doesn't have to be a chore! In fact, it can be downright magical. We're here to share some simple yet impressive math tricks that will not only boost your child's confidence but also make learning numbers a whole lot more fun. Perfect for elementary school kids, these tricks are designed to make math engaging and accessible.

Table of Contents

Multiplication Tricks:

Advanced features

Settings

F.A.Q. - (Frequently Asked Questions)

"Multiplication Tricks"

Multiplication Chart (1-10)

Times table chart 1 to 10 or the multiplication chart 1 to 10 is the chart that contains tables from 1 to 10 in a tabular format. In the table, the first row contains all the numbers for which we have to write the table i.e. the number from 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 and the first column contains the numbers for which the multiplication table is found, i.e. 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Then each column in the table contains the product of the number from the corresponding first row and first column.

x 1 2 3 4 5 6 7 8 9 10
1 1 2 3 4 5 6 7 8 9 10
2 2 4 6 8 10 12 14 16 18 20
3 3 6 9 12 15 18 21 24 27 30
4 4 8 12 16 20 24 28 32 36 40
5 5 10 15 20 25 30 35 40 45 50
6 6 12 18 24 30 36 42 48 54 60
7 7 14 21 28 35 42 49 56 63 70
8 8 16 24 32 40 48 56 64 72 80
9 9 18 27 36 45 54 63 72 81 90
10 10 20 30 40 50 60 70 80 90 100

Multiplication Chart (11-20)

Times table chart 11 to 20 or the multiplication chart 11 to 20 is the chart that contains tables from 11 to 20 in a tabular format. In the table, the first row contains all the numbers for which we have to write the table i.e. the number from 11, 12, 13, 14, 15, 16, 17, 18, 19, and 20 and the first column contains the numbers for which the multiplication table is found, i.e. 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Then each column in the table contains the product of the number from the corresponding first row and first column.

x 11 12 13 14 15 16 17 18 19 20
1 11 12 13 14 15 16 17 18 19 20
2 22 24 26 28 30 32 34 36 38 40
3 33 36 39 42 45 48 51 54 57 60
4 44 48 52 56 60 64 68 72 76 80
5 55 60 65 70 75 80 85 90 95 100
6 66 72 78 84 90 96 102 108 114 120
7 77 84 91 98 105 112 119 126 133 140
8 88 96 104 112 120 128 136 144 152 160
9 99 108 117 126 135 144 153 162 171 180
10 110 120 130 140 150 160 170 180 190 200

Multiplication Chart (21-30)

Times table chart 21 to 30 or the multiplication chart 21 to 30 is the chart that contains tables from 21 to 30 in a tabular format. In the table, the first row contains all the numbers for which we have to write the table i.e. the number from 21, 22, 23, 24, 25, 26, 27, 28, 29, and 30 and the first column contains the numbers for which the multiplication table is found, i.e. 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Then each column in the table contains the product of the number from the corresponding first row and first column.

x 21 22 23 24 25 26 27 28 29 30
1 21 22 23 24 25 26 27 28 29 30
2 42 44 46 48 50 52 54 56 58 60
3 63 66 69 72 75 78 81 84 87 90
4 84 88 92 96 100 104 108 112 116 120
5 105 110 115 120 125 130 135 140 145 150
6 126 132 138 144 150 156 162 168 174 180
7 147 154 161 168 175 182 189 196 203 210
8 168 176 184 192 200 208 216 224 232 240
9 189 198 207 216 225 234 243 252 261 270
10 210 220 230 240 250 260 270 280 290 300

Memorize the 9 Tables

This classic trick is a fantastic way to master the 9 times table without memorizing every single fact.

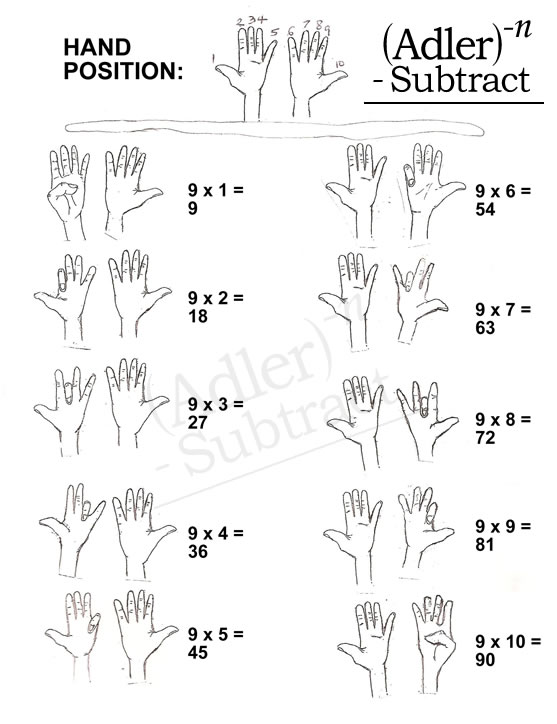Main Screen How it works:

  • Hold both hands out in front of you, palms facing away.
  • To multiply 9 by a number (let's say 9 x 3), count from the left, and fold down the third finger.
  • The fingers to the left of the folded finger represent the tens (in this case, 2).
  • The fingers to the right represent the ones (in this case, 7).
  • So, 9 x 3 = 27.
  • This works for 9 multiplied by any number from 1 to 10.
Why it's great: It provides a visual and kinesthetic way to understand multiplication, making it easier to remember.


Prime Factorization

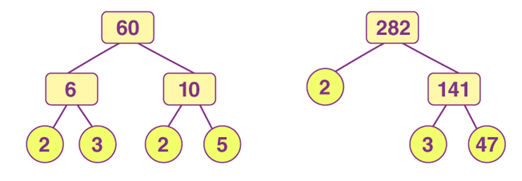
Main Screen

In the figure, we can show how number 60 is first factorized into two numbers i.e. 6 and 10.

  • Again, 6 and 10 is factorized to get the prime factors of 6 and 10, such that;
  • 6 = 2 × 3
  • and 10 = 2 × 5
  • If we write the prime factors of 60 altogether, then;
  • Prime factorization of 60 = 6 × 10 = 2 × 3 × 2 × 5
  • Same is the case for number 282, such as;
  • 282 = 2 × 141 = 2 × 3 × 47
So in both cases, a tree structure is formed.

A common trick for prime factorization, especially when dealing with larger numbers, is to start by trying the smallest prime numbers (2, 3, 5, 7, 11, etc.) as divisors. This method, known as trial division, can quickly identify prime factors if the number is divisible by them. Another helpful tip is to use divisibility rules for the smaller primes, which can speed up the process of finding divisors.

Here's a breakdown of the process:

  • Start with the smallest prime:
    Begin by checking if the number is divisible by 2 (even numbers), then 3 (if the sum of digits is divisible by 3), and so on.
  • Use divisibility rules:
    Divisibility rules for 2, 3, 5, 11, and others can help you quickly determine if a number is divisible by those primes.
  • Continue with larger primes:
    Once you've checked the smaller primes and found a factor, divide the number by that factor and repeat the process with the new quotient.
  • Stop when you reach prime factors:
    Continue dividing by prime numbers until you are left with only prime factors.
  • Combine the prime factors:
    The prime factorization is the product of all the prime factors you found.

Example:

    Let's say you want to find the prime factorization of 72.
  • 72 is even, so it's divisible by 2: 72 ÷ 2 = 36.
  • 36 is also even, so it's divisible by 2: 36 ÷ 2 = 18.
  • 18 is even, so it's divisible by 2: 18 ÷ 2 = 9.
  • 9 is divisible by 3: 9 ÷ 3 = 3.
  • 3 is a prime number.
  • Therefore, the prime factorization of 72 is 2 × 2 × 2 × 3 × 3, or 23 x 32.

Factor Tree Method
To find the prime factorization of the given number using factor tree method, follow the below steps:
  • Step 1: Consider the given number as the root of the tree
  • Step 2: Write down the pair of factors as the branches of a tree
  • Step 3: Again factorize the composite factors, and write down the factors pairs as the branches
  • Step 4: Repeat the step, until to find the prime factors of all the composite factors
In factor tree, the factors of a number are found and then those numbers are further factorized until we reach the closure.


Positive Divisor Of Large Number

Let us learn this trick of how to find quickly all positive divisors of a large number. As an example let us find all positive divisors of 1980.

To find the number of divisors of a number, we can prime factorize the number and use the formula (a1+1),(a2+1)...(ak+1), where (a1,a2,... ,ak) are the exponents in the prime factorization.Β 

How to solve?

To prime factorize 1980 we use the formula mentioned above..Β 

Step 1: Prime factorize 1980

  • 1980 = 2 × 990
  • 990 = 2 × 495
  • 495 = 5 × 99
  • 99 = 9 × 11
  • 9 = 3 × 3
  • So 1980 = 2 × 2 × 3 × 3 × 5 × 11 = 22×32×51×111.

Step 2: Use the formula above to find the number of divisors

  • The exponents are 2, 2, 1 and 1
  • Thus the number of divisors are (2 + 1) × (2 + 1) × (1 + 1) × (1 + 1)
  • (3)×(3)×(2)×(2) = 36

The number of positive divisors of 1980 are 36

Hence, the factors of 1980 are 1, 2, 3, 4, 5, 6, 9, 10, 11, 12, 15, 18, 20, 22, 30, 33, 36, 44, 45, 55, 60, 66, 90, 99, 110, 132, 165, 180, 198, 220, 330, 396, 495, 660, 990, 1980.



Probability

Many events can't be predicted with total certainty. The best we can say is how likely they are to happen, using the idea of probability.

Main Screen

When a coin is tossed, there are two possible outcomes: Heads (H) or Tails (T)

  • the probability of the coin landing H is 1⁄2
  • the probability of the coin landing T is 1⁄2

    • Main Screen

    When a single die is thrown, there are six possible outcomes: 1, 2, 3, 4, 5, 6

  • the probability of getting any one of them is 1⁄6

    • Probability Question

    John rolls 3 standard 6 sided dice 2 red and 1 yellow what is the probability that the numbers rolled on the red dices are both greater than the number rolled on the yellow die?

    Let's calculate this step by step:

    • Understand the dice rolls: Each die has 6 faces (numbers 1 through 6). John rolls two red dice and one yellow die.
    • Key condition: Both numbers rolled on the red dice must be greater than the number rolled on the yellow die.
    • Total outcomes: Since each die roll is independent, there are a total of 6 × 6 × 6 = 216 possible outcomes.
    • Counting favorable outcomes:
      • Let the number rolled on the yellow die be π‘Œ, and the numbers on the red dice be 𝑅1 and 𝑅2.
      • To satisfy the condition 𝑅1 > π‘Œ and 𝑅2 > π‘Œ, we need to count how many values 𝑅1 and 𝑅2 can take for each possible π‘Œ.
    • Let's find all possible outcomes,
      • If π‘Œ = 1: Both 𝑅1 and 𝑅2 can be any of 2,3,4,5,6. That’s 5 × 5 = 25 outcomes.
      • If π‘Œ = 2: 𝑅1 and 𝑅2 can be any of 3,4,5,6. That’s 4 × 4 = 16 outcomes.
      • If π‘Œ = 3: 𝑅1 and 𝑅2 can be any of 4,5,6. That’s 3 × 3 = 9 outcomes.
      • If π‘Œ = 4: 𝑅1 and 𝑅2 can be any of 5,6. That’s 2 × 2 = 4 outcomes.
      • If π‘Œ = 5: 𝑅1 and 𝑅2 can only be 6. That’s 1 × 1 = 1 outcome.
      • If π‘Œ = 6: 𝑅1 and 𝑅2 can't be greater than π‘Œ. So 0 outcomes.
    • Sum of favorable outcomes: 25 + 16 + 9 + 4 + 1 = 55
    • Probability: The probability is the ratio of favorable outcomes to total outcomes:

      Probability = Favorable OutcomesTotal Outcomes = 55216

    Final Answers
    The probability is 55216, which is approximately 0.2546 or 25.46%.



    Diagonals In A Polygon

    A polygon with n sides has n(n-3)2diagonals. This formula can be derived by considering that each vertex can connect to n-3 other vertices to form a diagonal, and then accounting for the fact that each diagonal is counted twice (once for each endpoint).

    Explanation:

  • Total Connections: In a polygon with n sides, there are n vertices. Each vertex can be connected to every other vertex, which would result in n(n-1)/2 connections.
  • Subtracting sides: However, n of these connections are the sides of the polygon, not diagonals.
  • Subtracting diagonals: Therefore, the number of diagonals is the total number of connections minus the number of sides: n(n-1)/2 - n.
  • Simplifying: This simplifies to n(n-3)/2.



    • Divisibility Rules

    Division is a mathematical operation used to distribute a quantity into equal parts or to find out how many times one number (the divisor) is contained within another number (the dividend). The result of division is called the quotient.

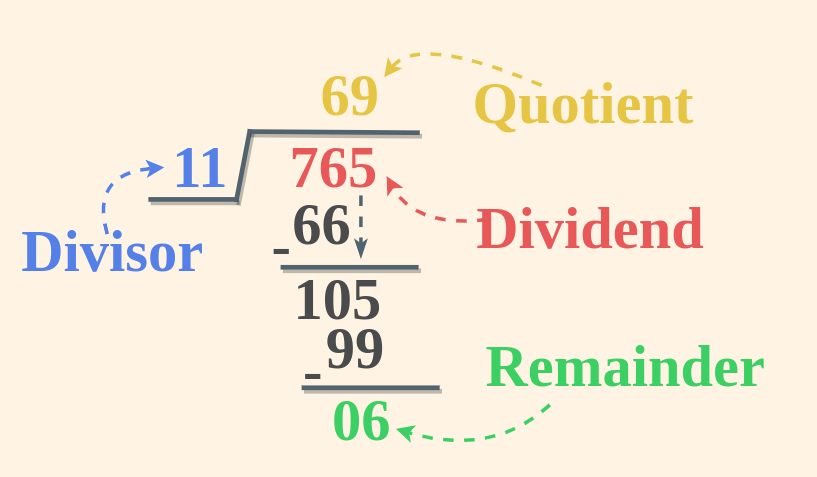
    Main Screen

    The formula for division is: Quotient = DivisorDividend

    Easy Division Tricks

    Here are easy division tricks to fasten your calculation:

    Divisible By Conditions Examples
    2 Last digit is 0,2,4,6,8 132, 100, 12
    3 Sum of the digits is divisible by 3 4764; 4+7+6+4 = 21
    21⁄3 = 7
    4 Last 2 digits are divisible by 4 1924
    24⁄4 = 6
    5 Last digit is 0 or 5 255, 1970
    6 Number is divisible by both 2 and 3 7782; 7+7+8+2 = 24
    24⁄3 = 8
    7 Double the unit digit and subtract it from the rest of the number. The reusltign number must be divisible by 7. 385; 38 − (2 × 5) = 28
    28⁄7 = 4
    8 A number is divisible by 8 if the number formed by its last three digits is divisible by 8 1320
    320⁄8 = 40
    9 Sum of all its digits is divisible by 9 288; 2+8+8 = 18
    18⁄9 = 2
    10 Last digit is 0 8070


    Advanced features

    Game Statistics

    Item as IconThere are multiple ways we could have collected the game statistics. We decided to highlight the most important one which anytime some one plays a puzzle may want to look for!

    We decided to choose the total game timer has the most effect hence the same is translated as the best representation of your fast but critical thinking. Additionally we do list out the total moves and the player primary color choice (reserved for advance game plays with full setup)

    Tip: Game statistics are valuable tools to analyze your playing prowess. We have purposefully concentrated on the total game times as the best tool to see if you could think critically in the most effective way but in the shortest possible times. Compare these timings with your friends and certainly boast about your best times.


    Settings

    Delete All Saved Game Statistics

    Item as IconSometimes you may have a need where you wish to just reset! For this very purpose we have created the button for deleting all saved game statistics. This action permanently deletes all saved game statistics from your mobile device permanently.

    Tip: Button click on 'Erase All Game Statistics' is a permanent action meaning data is permanently lost and can't be recovered in any circumstances by the King Slayer Chess mobile app.

    Frequently Asked Questions

    Here is the list of popularly asked questions related to King Slayer Chess app series. While we have tried answering all questions to best of our abilities, there may be an opportunity of an improvement. Please don't hesitate to ask any questions. We will try our level best to answer the same as-soon-as-possible (ASAP).

    This is related to how mobile applications render a visible screen. They usually get attached/instantiated once and then await it's destruction usually at the closing of the mobile application itself. Subsequent start of the same mobile application will load all saved data immediately though. Alternatively, we have designed a page refresh option by simply pulling down on your game statistics screen to refresh your screen and display any new saved game statistics. We don't copy any data outside of your mobile app in King Slayer Chess series hence all data is maintained locally.

    Ofcourse, we carefully developed multiple chess puzzle packs each pushing you to allow more critical thinking. While, some puzzles may sound very easy to you but we guarantee you some puzzles will certainly make you think harder. Look out for more puzzle packs in your mobile app store. We don't display any advertisements hence your game play is uninterrupted and your game playing experience will allow you to play your best move.

    Our game experience is designed to be played in same fashion in both Android and Apple devices. You may select light mode or dark mode selections as per your devices settings. The same King Slayer Chess puzzle packs are available in Android and Apple supported devices. The tablet playing experience is more rewarding due to bigger screen sizes. Hence do try the iPad/tablet experience.